1. What is the Specific Gas Constant Calculator?

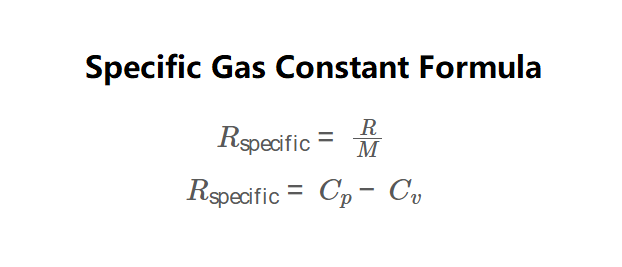
Definition: This calculator computes the specific gas constant (\( R_{\text{specific}} \)) for a gas or mixture, used in thermodynamic equations like the ideal gas law (\( P = \rho R_{\text{specific}} T \)). It supports two methods, as shown in the formula image above:

• Molar Mass Method: \( R_{\text{specific}} = \frac{R}{M} \), where \( R \) is the universal gas constant and \( M \) is the molar mass.
• Specific Heat Method: \( R_{\text{specific}} = C_p - C_v \), where \( C_p \) and \( C_v \) are specific heats at constant pressure and volume.

Users can select output units (J/(kg·K), kJ/(kg·K), cal/(g·K)) interactively.

Purpose: Essential for engineers, scientists, and students in thermodynamics, aerodynamics, and chemical engineering to analyze gas behavior.

2. How Does the Calculator Work?

The specific gas constant is calculated using one of two formulas, as depicted in the formula image:

\( R_{\text{specific}} = \frac{R}{M} \quad \text{or} \quad R_{\text{specific}} = C_p - C_v \)

Where:

• \( R_{\text{specific}} \): Specific gas constant (J/(kg·K));
• \( R \): Universal gas constant, default 8.31446261815324 J/(mol·K);
• \( M \): Molar mass (g/mol or kg/mol);
• \( C_p \): Specific heat at constant pressure (J/(kg·K));
• \( C_v \): Specific heat at constant volume (J/(kg·K)).

Available Gases and Molar Masses:

Gas	Molar Mass (g/mol)
Air	28.96
Nitrogen	28.02
Oxygen	32.00
Carbon Dioxide	44.01
Custom	User-defined

Steps:

• Select the calculation method (molar mass or specific heat).
• For molar mass method:
  • Choose a gas (e.g., Air) or select "Custom" to enter molar mass.
  • Enter molar mass in g/mol or kg/mol.
• For specific heat method:
  • Enter \( C_p \) and \( C_v \) in J/(kg·K).
• Enter the universal gas constant (\( R \)), defaulting to 8.31446261815324 J/(mol·K).
• Submit to calculate \( R_{\text{specific}} \).
• Change the output unit (J/(kg·K), kJ/(kg·K), cal/(g·K)) to convert the result instantly.
• Results are formatted to 2 decimal places, with scientific notation for values less than 0.001.

3. Importance of Specific Gas Constant

The specific gas constant is critical for:

• Thermodynamics: Calculating gas properties like density and heat capacity.
• Engineering: Designing engines, HVAC systems, and gas pipelines.
• Aerodynamics: Modeling gas behavior in propulsion or high-altitude flight.

4. Using the Calculator

Example 1: Calculate the specific gas constant for air using the molar mass method, with \( R = 8.31446261815324 \, \text{J/(mol·K)} \), output in J/(kg·K):

• Method: Molar Mass
• Gas: Air (\( M = 28.96 \, \text{g/mol} = 0.02896 \, \text{kg/mol} \))
• Calculation: \( R_{\text{specific}} = \frac{8.31446261815324}{0.02896} \approx 287.17 \, \text{J/(kg·K)} \)

Results:

• Specific Gas Constant: 287.17 J/(kg·K)

Example 2: Calculate the specific gas constant for a gas with \( C_p = 1005 \, \text{J/(kg·K)} \), \( C_v = 718 \, \text{J/(kg·K)} \), output in kJ/(kg·K):

• Method: Specific Heat
• \( C_p = 1005 \, \text{J/(kg·K)} \), \( C_v = 718 \, \text{J/(kg·K)} \)
• Calculation: \( R_{\text{specific}} = 1005 - 718 = 287 \, \text{J/(kg·K)} = 0.287 \, \text{kJ/(kg·K)} \)

Results:

• Specific Gas Constant: 0.29 kJ/(kg·K)

5. Frequently Asked Questions (FAQ)

Q: What is the specific gas constant?
A: It’s a gas-specific constant used in the ideal gas law (\( P = \rho R_{\text{specific}} T \)), relating pressure, density, and temperature.

Q: When to use the molar mass vs. specific heat method?
A: Use molar mass for known gases or mixtures with defined molar masses. Use specific heat for gases where \( C_p \) and \( C_v \) are measured, especially mixtures.

Q: Why must \( C_p > C_v \)?
A: Thermodynamics requires \( C_p > C_v \) because work is done by a gas at constant pressure, increasing its heat capacity.

Q: Is this calculator valid for real gases?
A: Yes, for low-density, high-temperature conditions where ideal gas assumptions hold. For high pressures, consider real gas corrections.

Q: Can I modify the universal gas constant?
A: Yes, the default is 8.31446261815324 J/(mol·K), but you can edit it for custom calculations.

Specific Gas Constant Calculator © - All Rights Reserved 2025