1. What is the Molar Mass of Gas Calculator?

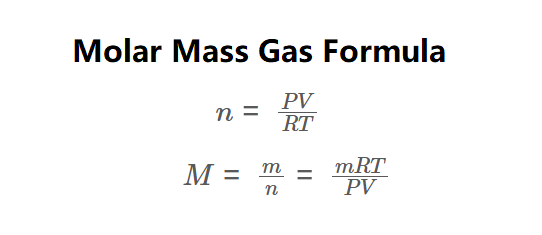
Definition: This calculator computes the number of moles (\( n \)) and molar mass (\( M \)) of a gas using the ideal gas law, as shown in the formula image above. Moles and molar mass are calculated via:

\( n = \frac{PV}{RT}, \quad M = \frac{m}{n} = \frac{mRT}{PV} \)

Users input mass (\( m \)), volume (\( V \)), pressure (\( P \)), and temperature (\( T \)), with support for multiple units. Results are displayed with 5 decimal places for precision, with moles in mol and molar mass in g/mol or kg/mol.

Purpose: Essential for chemistry and chemical engineering to determine the quantity and identity of gases, perform stoichiometric calculations, and understand gas behavior in reactions or processes.

2. How Does the Calculator Work?

The calculator uses the ideal gas law (\( PV = nRT \)) to calculate moles (\( n \)) and molar mass (\( M \)):

\( n = \frac{PV}{RT}, \quad M = \frac{m}{n} = \frac{mRT}{PV} \)

Where:

• \( n \): Number of moles (mol);
• \( M \): Molar mass (g/mol, kg/mol);
• \( m \): Mass (g, kg, mg, oz, lb);
• \( V \): Volume (m³, mm³, cm³, ml, L, cu ft, in³);
• \( P \): Pressure (Pa, kPa, atm, bar, psi, mmHg);
• \( T \): Temperature (K, °C, °F);
• \( R \): Universal gas constant, default 8.31446261815324 J/(mol·K).

Common Gases and Molar Masses:

Gas	Molar Mass (g/mol)
Air	28.96
Nitrogen (N₂)	28.02
Oxygen (O₂)	32.00
Carbon Dioxide (CO₂)	44.01
Methane (CH₄)	16.04
Chlorine (Cl₂)	70.91

Steps:

• Enter mass with units (g, kg, mg, oz, lb).
• Enter volume with units (m³, mm³, cm³, ml, L, cu ft, in³).
• Enter pressure with units (Pa, kPa, atm, bar, psi, mmHg).
• Enter temperature with units (K, °C, °F).
• Enter the universal gas constant (\( R \)), defaulting to 8.31446261815324 J/(mol·K).
• Submit to calculate moles and molar mass.
• Change the molar mass output unit (g/mol, kg/mol) to convert the result instantly.
• Results are formatted to 5 decimal places, with scientific notation for values less than 0.001.

3. Importance of Molar Mass and Moles Calculation

Calculating moles and molar mass is critical for:

• Chemistry: Identifying unknown gases, quantifying substances, and performing stoichiometric calculations.
• Chemical Engineering: Designing reactors and optimizing gas processes.
• Environmental Science: Analyzing gas compositions in air quality studies.

4. Using the Calculator

Example 1: Calculate the moles and molar mass of a gas with 0.04268 oz mass, 677 ml volume, 0.987 atm pressure, and 23°C temperature, with \( R = 8.31446261815324 \, \text{J/(mol·K)} \), output in mol, g/mol, and kg/mol:

• Mass: \( m = 0.04268 \, \text{oz} = 0.04268 \div 35.27396195 \approx 0.001211 \, \text{kg} \)
• Volume: \( V = 677 \, \text{ml} = 0.000677 \, \text{m³} \)
• Pressure: \( P = 0.987 \, \text{atm} = 0.987 \times 101325 = 99907.725 \, \text{Pa} \)
• Temperature: \( T = 23 \, \text{°C} = 296.15 \, \text{K} \)
• Moles: \( n = \frac{99907.725 \times 0.000677}{8.31446261815324 \times 296.15} \approx 0.02746 \, \text{mol} \)
• Molar Mass: \( M = \frac{0.001211}{0.02746} \approx 0.04407 \, \text{kg/mol} = 44.07426 \, \text{g/mol} \)
• Unit conversion: \( 0.04407 \, \text{kg/mol} \)

Results:

• Moles: 0.02746 mol
• Molar Mass: 44.07426 g/mol
• Molar Mass (converted): 0.04407 kg/mol

Note: The molar mass (~44 g/mol) suggests the gas could be CO₂ (44.01 g/mol).

Example 2: Calculate the moles and molar mass of a gas with 0.03086 lb mass, 183.07 in³ volume, 650 mmHg pressure, and 300 K temperature, output in mol, g/mol, and kg/mol:

• Mass: \( m = 0.03086 \, \text{lb} = 0.03086 \div 2.2046226218 \approx 0.014 \, \text{kg} \)
• Volume: \( V = 183.07 \, \text{in³} = 183.07 \div 61023.7441 \approx 0.003 \, \text{m³} \)
• Pressure: \( P = 650 \, \text{mmHg} = 650 \times 133.322368 = 86659.5392 \, \text{Pa} \)
• Temperature: \( T = 300 \, \text{K} \)
• Moles: \( n = \frac{86659.5392 \times 0.003}{8.31446261815324 \times 300} \approx 0.10424 \, \text{mol} \)
• Molar Mass: \( M = \frac{0.014}{0.10424} \approx 0.13424 \, \text{kg/mol} = 134.24180 \, \text{g/mol} \)
• Unit conversion: \( 0.13424 \, \text{kg/mol} \)

Results:

• Moles: 0.10424 mol
• Molar Mass: 134.24180 g/mol
• Molar Mass (converted): 0.13424 kg/mol

5. Frequently Asked Questions (FAQ)

Q: What is molar mass?
A: Molar mass is the mass of one mole of a substance, typically expressed in grams per mole, crucial for chemical calculations involving gases.

Q: Why use the ideal gas law for molar mass?
A: The ideal gas law relates measurable properties like mass, volume, pressure, and temperature to calculate the molar mass of an unknown gas.

Q: Why is Kelvin required for temperature?
A: Kelvin ensures positive absolute temperatures for accurate ideal gas law calculations.

Q: Does this work for real gases?
A: Yes, for low pressures and high temperatures where ideal gas assumptions hold. For high pressures, real gas corrections may be needed, such as using the van der Waals equation.

Q: Can I change the universal gas constant?
A: Yes, the default value is 8.31446261815324 joules per mole per Kelvin, but you can edit it for custom calculations.

Molar Mass of Gas Calculator © - All Rights Reserved 2025