Ideal Gas Temperature Calculator

Pressure (\( P \)):

Volume (\( V \)):

Number of Moles (\( n \)): mol

1. What is the Ideal Gas Temperature Calculator?

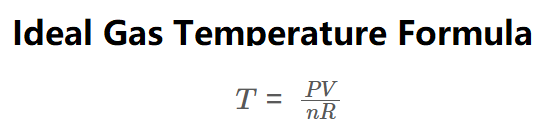
Definition: This calculator computes the temperature (\( T \)) of an ideal gas using the ideal gas law. As shown in the formula image above, temperature is calculated via:

\( T = \frac{PV}{nR} \)

Users input pressure, volume, and number of moles, selecting appropriate units. Results are displayed with 5 decimal places in Kelvin, Celsius, or Fahrenheit.

Purpose: Essential for thermodynamics, physics, and engineering to determine gas temperature in applications like HVAC systems, gas storage, and laboratory experiments.

2. How Does the Calculator Work?

The calculator derives gas temperature from the ideal gas law (\( PV = nRT \)), rearranged as:

\( T = \frac{PV}{nR} \)

Where:

\( T \): Temperature (K, °C, °F);
\( P \): Pressure (Pa, kPa, atm, bar, psi, mmHg);
\( V \): Volume (m³, L, mm³, cm³, mL, in³, ft³);
\( n \): Number of moles (mol);
\( R \): Universal gas constant, 8.31446261815324 J/(mol·K).

Steps:

Enter pressure with units (Pa, kPa, atm, bar, psi, mmHg).
Enter volume with units (m³, L, mm³, cm³, mL, in³, ft³).
Enter the number of moles.
Submit to calculate temperature.
Change the output unit (K, °C, °F) to convert the result instantly.
Results are formatted to 5 decimal places, with scientific notation for values less than 0.001.

3. Importance of Ideal Gas Temperature Calculation

Gas temperature calculations are critical for:

Thermodynamics: Analyzing energy transfer in engines and refrigerators.
Chemical Engineering: Controlling reaction conditions in gas-phase processes.
Meteorology: Understanding atmospheric behavior.

4. Using the Calculator

Example 1: Calculate the temperature of 1 mol of gas at 1 atm pressure and 22.4 L volume, output in K and °C:

Pressure: \( P = 1 \, \text{atm} = 101325 \, \text{Pa} \)
Volume: \( V = 22.4 \, \text{L} = 0.0224 \, \text{m}^3 \)
Moles: \( n = 1 \, \text{mol} \)
Calculation: \( T = \frac{101325 \times 0.0224}{1 \times 8.31446261815324} \approx 273.15000 \, \text{K} \)
Unit conversion: \( 273.15 \, \text{K} = 0.00 \, \text{°C} \)

Results:

Temperature: 273.15000 K
Temperature (converted): 0.00000 °C

Example 2: Calculate the temperature of 0.5 mol of gas at 2 bar pressure and 0.01 m³ volume, output in K and °F:

Pressure: \( P = 2 \, \text{bar} = 200000 \, \text{Pa} \)
Volume: \( V = 0.01 \, \text{m}^3 \)
Moles: \( n = 0.5 \, \text{mol} \)
Calculation: \( T = \frac{200000 \times 0.01}{0.5 \times 8.31446261815324} \approx 480.90643 \, \text{K} \)
Unit conversion: \( 480.90643 \times 9/5 - 459.67 \approx 405.63177 \, \text{°F} \)

Results:

Temperature: 480.90643 K
Temperature (converted): 405.63177 °F

5. Frequently Asked Questions (FAQ)

Q: What is the ideal gas law?
A: The ideal gas law, \( PV = nRT \), relates pressure, volume, temperature, and moles of an ideal gas, assuming no intermolecular forces and elastic collisions.

Q: Why use Kelvin for calculations?
A: Kelvin ensures positive temperatures, aligning with the ideal gas law’s requirements. The calculator converts to °C or °F for convenience.

Q: Is this calculator valid for real gases?
A: Yes, for gases like air, nitrogen, or oxygen at high temperatures and low pressures, where ideal gas behavior is a good approximation.

Q: What if I don’t know the number of moles?
A: You can estimate moles using mass and molar mass or measure gas quantity experimentally.

Favorite