1. What is the Ideal Gas Density Calculator?

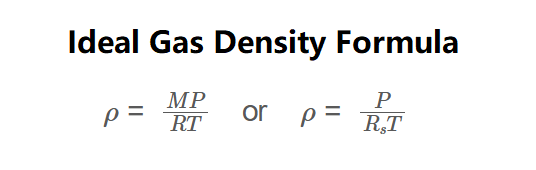
Definition: This calculator computes the density (\( \rho \)) of an ideal gas, defined as mass per unit volume (\( \rho = \frac{m}{V} \)), using the ideal gas law. As shown in the formula image above, density is calculated via:

\( \rho = \frac{MP}{RT} \quad \text{or} \quad \rho = \frac{P}{R_s T} \)

Users select a substance or enter custom molar mass and specific gas constant, along with pressure and temperature. Results are displayed with 5 decimal places in kg/m³ or other units.

Purpose: Essential for thermodynamics, aerodynamics, and chemical engineering to analyze gas behavior in applications like aircraft design or gas transport systems.

2. How Does the Calculator Work?

The calculator derives gas density from the ideal gas law (\( PV = nRT \)), where \( n = \frac{m}{M} \), rearranged as:

\( \rho = \frac{MP}{RT} \quad \text{or} \quad \rho = \frac{P}{R_s T} \)

Where:

• \( \rho \): Density (kg/m³, g/L, lb/ft³, g/cm³, kg/cm³, mg/cm³, g/m³, g/dm³);
• \( M \): Molar mass (kg/mol);
• \( P \): Pressure (Pa, kPa, atm, bar, psi, mmHg);
• \( T \): Temperature (K, °C, °F);
• \( R \): Universal gas constant, 8.31446261815324 J/(mol·K);
• \( R_s \): Specific gas constant (J/(kg·K)).

Available Substances and Properties:

Substance	Molar Mass (g/mol)	Specific Gas Constant (J/(kg·K))
Air	28.97	287.1
Argon	39.95	208.1
Butane	58.12	143.1
Carbon dioxide	44.01	188.9
Carbon monoxide	28.01	296.8
Ethane	30.07	276.5
Ethylene	28.05	296.3
Helium	4	2078.6
Hydrogen	2.02	4119
Methane	16.04	518.3
Neon	20.18	411.9
Nitrogen	28.01	296.8
Octane	114.23	72.8
Oxygen	32	259.8
Propane	44.1	188.6
Steam (Water vapor)	18.02	461.5
Custom	User-defined	User-defined

Steps:

• Select a substance from the list (showing molar mass and specific gas constant) or choose "Custom" to enter your own values.
• If custom, enter molar mass in g/mol or kg/mol and specific gas constant in J/(kg·K).
• Enter pressure with units (Pa, kPa, atm, bar, psi, mmHg).
• Enter temperature with units (K, °C, °F).
• Submit to calculate density.
• Change the output unit (kg/m³, g/L, lb/ft³, g/cm³, kg/cm³, mg/cm³, g/m³, g/dm³) to convert the result instantly.
• Results are formatted to 5 decimal places, with scientific notation for values less than 0.001.

3. Importance of Ideal Gas Density Calculation

Gas density calculations are critical for:

• Aerodynamics: Determining lift and drag in aircraft or balloon design.
• Chemical Engineering: Designing reactors and gas transport systems.
• Environmental Science: Analyzing atmospheric gas behavior.

4. Using the Calculator

Example 1: Calculate the density of air at 1 atm and 20°C, output in kg/m³ and g/L:

• Substance: Air (\( M = 28.97 \, \text{g/mol} = 0.02897 \, \text{kg/mol}, R_s = 287.1 \, \text{J/(kg·K)} \))
• Pressure: \( P = 1 \, \text{atm} = 101325 \, \text{Pa} \)
• Temperature: \( T = 20 \, \text{°C} = 293.15 \, \text{K} \)
• Calculation: \( \rho = \frac{0.02897 \times 101325}{8.31446261815324 \times 293.15} \approx 1.20466 \, \text{kg/m}^3 \)
• Unit conversion: \( 1.20466 \, \text{kg/m}^3 = 1.20466 \, \text{g/L} \)

Results:

• Density: 1.20466 kg/m³
• Density (converted): 1.20466 g/L

Example 2: Calculate the density of a custom gas with molar mass 50 g/mol and specific gas constant 166.3 J/(kg·K) at 2 atm and 25°C, output in kg/m³ and lb/ft³:

• Substance: Custom (\( M = 50 \, \text{g/mol} = 0.05 \, \text{kg/mol}, R_s = 166.3 \, \text{J/(kg·K)} \))
• Pressure: \( P = 2 \, \text{atm} = 2 \times 101325 = 202650 \, \text{Pa} \)
• Temperature: \( T = 25 \, \text{°C} = 298.15 \, \text{K} \)
• Calculation: \( \rho = \frac{0.05 \times 202650}{8.31446261815324 \times 298.15} \approx 4.08518 \, \text{kg/m}^3 \)
• Unit conversion: \( 4.08518 \times 0.062428 \approx 0.25507 \, \text{lb/ft}^3 \)

Results:

• Density: 4.08518 kg/m³
• Density (converted): 0.25507 lb/ft³

5. Frequently Asked Questions (FAQ)

Q: What is gas density?
A: Gas density is the mass of a gas per unit volume, typically in kg/m³, calculated using the ideal gas law.

Q: How do I select a substance?
A: Choose a predefined substance from the dropdown, which shows its molar mass and specific gas constant, or select "Custom" to enter your own values.

Q: Why use absolute temperature?
A: The ideal gas law requires temperature in Kelvin to ensure positive values and accurate calculations.

Q: Is this calculator valid for real gases?
A: Yes, for low pressures and high temperatures where ideal gas assumptions hold. For high pressures, real gas corrections may be needed.

Q: What is the specific gas constant?
A: The specific gas constant (\( R_s \)) is the universal gas constant divided by the molar mass of the gas, expressed in J/(kg·K).

Ideal Gas Density Calculator © - All Rights Reserved 2025